zum Selbststudium | zum Selbststudium |
Was ist Rekursion?
Wir unterscheiden zwei Arten:
Ein Mops kam in die Küche ... YouTube ;-)
Ein einprägsames Beispiel, allerdings fehlt hier die Abbruchbedingung, es sei denn, ein Meteoriteneinschlag würde der Mopspopulation ein jähes Ende bereiten.
Bei einer Matrjoschka (staubfangendes Mitbringsel aus Russland) ist die Abbruchbedingung durch die kleinste Puppe gegeben. Auch findet hier eine Vereinfachung dergestalt statt, dass jede kleinere Puppe stets weniger Puppen birgt. Sicher ist eine Matrjoschka für Kinder interessant, dabei gibt es jedoch kein Problem zu lösen. Rekursive Definition: Eine Matrjoschka ist eine Figur, die eine Matrjoschka enthält, oder Klara (unzerlegbare Figur). Klara ist die Abbruchbedingung ;-).
Summe der ersten n natürlichen ZFakultätsfunktion
6! = 1 x 2 x 3 x 4 x 5 x 6 = 720
Die Fakultät einer natürlichen Zahl ist das Produkt aller Zahlen von der 1 bis zur Zahl selbst.
n! = n * (n-1)!, falls n > 1
Rekursiv gerechnet sieht das so aus:
6! = 6 x 5!
5! = 5 x 4!
4! = 4 x 3!
3! = 3 x 2!
2! = 2 x 1!
1! = 1
Beispiel
Rechner zur Berechnung der Fakultät (Gib zum Beispiel 5! ein!)
Hefteintrag
Programm zur (rekursiven) Berechnung der Fakultät
Quelltext
public class Fakultaet{
int factr(int x){
if (x==1) return 1;
else{
return x*factr(x-1);
}
}
}
Weitere Beispiele mit Java-Code (auch iterativ) finden Sie hier:
f(n) = n! 1 * 2 * ... * * n = f(n-1) * n
Algorithmus
1. Eingabe n,k (n>=k>=0)
2. Falls k=n oder k=0 gilt (Trivialfall), weiter mit Schritt 3
3. binoko = 1
4. Ansonsten weiter mit Schritt 5
5. binoko = binoko(n-1,k)+binoko(n-1,k-1)
6. Ausgabe binoko
Parallele Spiegel Sie befinden sich zwischen zwei parallel zueinander aufgestellten Spiegeln. Ein Spiegel gibt stets das wieder, was im gegenüberliegenden zu sehen ist.
| Bild im Bilde Mit dem Programm Teamviewer kann man auf einen anderen Computer zugreifen (Wartung, Hilfe). Stellen Sie nun Teamviewer so ein, dass der Partner auf Ihren Desktop schauen kann, ergibt sich nebenstehendes Bild. Leider ist dies - wie bei Beispiel e) - ein unendlicher Prozess, man kann zwar die ganz kleinen Bilder nicht mehr wahrnehmen, aber auf das Programmieren übertragen würde es dort zu einer Endlosschleife führen. Es gibt also keine logische Abbruchbedingung, die das Ganze stoppen würde. |
 |
Rekursion in der Informatik
Rekursion (von lateinisch recurrere = zurücklaufen) bezeichnet eine Methode in der Programmierung, in der sich eine Funktion selbst aufruft. Gegenstück: Iteration.Bei der Berechnung einer rekursiven Funktion wird der berechnete Wert eines Schleifendurchlaufs (Iteration) als Eingabe für den nächsten Durchlauf benötigt.
Die Idee ist also, ein Problem "auf sich selbst" zurückzuführen.
Die meisten Programmiersprachen unterstützen heute rekursive Funktionen. Man versucht im Normalfall, rekursive Funktionen zu vermeiden, da diese bei großer Rekursionstiefe viel Speicher auf dem Stack benötigen, was im Extremfall zu einem Überlauf führen kann.
Es gibt allerdings Problemstellungen, die sich mit Hilfe der Rekursion sehr elegant lösen lassen. Wichtig ist vor allem, dass jeder rekursive Algorithmus eine Abbruchbedingung enthält.
Ein rekursiver Algorithmus lässt sich immer in einen nicht rekursiven umschreiben.
Eine Prozedur heißt rekursiv, wenn ihre Definition auf sich selbst zurückgreift. Sie ist also die Zusammensetzung Z aus einer Grundanweisung G und der Prozedur P selbst :
P = Z ( G, P )
Überblick
Fibonacci-Zahlen Die Folge 1, 1, 2, 3, 5, 8, 13, 21, 34, ... heißt die Fibonacci-Folge. Dabei erhält man das nächste Glied der Folge, indem man die zwei davor stehenden Zahlen addiert. Die Bezeichnung Fibonacci-Folge stammt.vom französischen Mathematiker Edouard Lucas. Die Art der Definition, bei der man die Folgenglieder nacheinander bekommt, nennt man rekursiv.
Dividiert man eine (höhere) Zahl dieser Reihe durch ihren Vorgänger, phi = (sqrt(5)+1)/2 = 1.61803...
|
|
AB/Hefteintrag unter Verwendung von dieser Übersicht
Programm zur Erzeugung einer Liste von Fibonacci-Zahlen
Das goldene Rechteck  |
Die goldene Schnecke
|
| Das Rad des Theodosius
|
 ist ein rechtwinkliges, gleichschenkliges Dreieck mit der Scheitellänge 1. Seine Hypothenuse ist gleichzeitig Kathete des sich anschließenden rechtwinkligen Dreiecks. :  |
|
| Das Hasenproblem Diese Aufgabe stammt von Fibonacci selbst. Aufgabe des Fibonacci in Latein ;-) Hier wird gezeigt, wie sich der Quotient aus aktuellem Glied und seinem Vorgänger Phi nähert.
|
Bitte beachten Sie, dass es bei einer großen Anzahl an Reihen manchmal recht lange dauern kann, bevor das Javascript das Dreieck vollständig berechnet hat.
Aufgabe: Zeichnen Sie ein Pascalsches Dreieck bis zur 7. Zeile (Wurzel ist Zeile 0) ins Heft, bestimmen Sie die Binominalkoeffizienten von  |
Information
Türme von Hanoi |
 |
||
| Turm 1 mit n Scheiben abnehmenden Durchmessers | Turm 2 |
Zwischenlager | |
 Hefteintrag |
|||
| Hintergrund (1. Link) |
|||
Ziel: Bewegen aller Scheiben von Turm 1 nach Turm 2.
Randbedingungen:
-
Jede Scheibe darf nur "einzeln" von einem Turm zu einem anderen bewegt werden.
- Nur jeweils die oberste Scheibe darf bewegt werden.
-
Auf einem Turm darf niemals eine größere über einer kleineren Scheibe liegen.
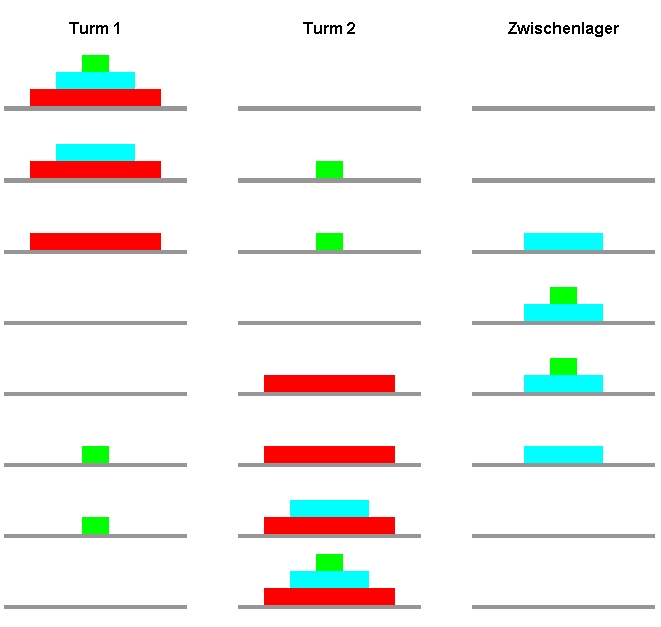
Das Problem wird jetzt in drei Teilprobleme zerlegt:
1. Lege n-1 Scheiben vom Turm 1 über Turm 2 auf das Zwischenlager.
2. Lege die letzte Scheibe direkt vom Turm 1 zum Turm 2.
3. Lege n-1 Scheiben vom Zwischenlager über Turm 1 zum Turm 2
Turm 1, Turm 2, Zwischenlager werden zyklisch durchlaufen.
Wenn ein Turm aus n Scheiben besteht, wird auf das zweimalige Versetzen eines aus n-1 Scheiben bestehenden Turmes zurückgeführt.
Der kürzeste Lösungsweg besteht bei n = 3 aus 2³ - 1 = 7 Zügen.
 |
// Nicht vergessen: Zuerst das Projekt speichern!
// Zuerst Doppelklick auf Start-Button, dann den Code der unten stehenden Prozedur Button1.Click schreiben,
anschließend den folgenden Code der Prozedur Bewege darüber schreiben
procedure Bewege ( n : integer; Turm1, Lager, Turm2 : ................... );
// Turm1 ist Ausgangsturm, Lager ist Zwischenlager, Turm2 ist Zielturm
begin
if n > 0 then // Wenn mindestens eine Scheibe vorhanden, dann beginne mit ....
begin
Bewege(n - 1,Turm1,Turm2,Lager); // Bewege n-1 Scheiben vom Turm 1 über Turm 2 auf das Zwischenlager.
Form1.Memo1.Lines.Add(Turm1 + ' ---> ' + Turm2); // wird im Memo-Feld angezeigt
Bewege(n - 1,Lager,Turm1,Turm2); // Bewege n-1 Scheiben vom Zwischenlager über Turm 1 zum Turm 2.
end;
end;
procedure TForm1.Button1Click(Sender: TObject);
var n : integer;
begin // Eingabe in ein Editfeld
n := StrToInt(Edit1.Text); // Variable n im Editfeld wird in Ganzzahl konvertiert.
Memo1.Clear; // Memo löschen (---> wiederholte Ausgabe)
Memo1.Text := ' '; // Leerzeile ausgeben
Bewege(n,'Turm1','Lager','Turm2') // Bewege n Scheiben vom Turm 1 über Zwischenlager auf Turm 2.
end;
Und hier ein JAVA-Quelltext
Anleitung für die Ausgabe
BlueJ öffnen >>> neues Projekt >>> Neue Klasse >>> Klassenname >>> Doppelklick auf Rechteck
Code eingeben/einfügen >>> Compilieren >>> Schließen >>> rechte Maustaste auf Rechteck
>>> void bewegeTurm >>>
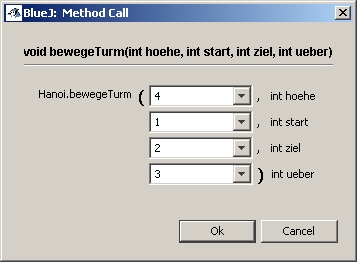
Einzufügender Quelltext
| public class Hanoi { private static int n = 5; public static void bewegeTurm(int hoehe, int turm1, int turm2, int lager) { if( n== 1 ) { // n = 1 System.out.println("bewege Scheibe von Turm " + turm1 + " nach Turm " + turm1); } else{ bewegeTurm(n-1, start, ueber, ziel); System.out.println("bewege Scheibe von Turm " + start + " nach Turm " + turm1); bewegeTurm(n-1, lager, turm2, turm1); } } public static void main(String[] args) { bewegeTurm(n, 1, 3, 2); } } |
Struktogramm
Beispiel 1
Beispiel 2
Projekt 1
Projekt 2
Projekt 3 (mit Sound)
Aufgabe a): Der französische Mathematiker Edouard Lucas, der diese Turmgeschichte ersonnen hat, sprach von einem 64-Scheiben-Turm. |
 |
Drachenkurvenfraktal Quelle: Wikipedia |
|
Aufgabe a) Laden Sie das Programm "Fraktale Strukturen" herunter |
Aufgabe b) Wettbewerb: Falte ein A4-Blatt dann das Blatt jeweils in der Mitte und öffne es wieder so, dass die einzelnen Teile einen rechten Winkel bilden. Wie viele Faltungen = n bekommst du hin? |
