
Zu Beginn ein kleines Spiel (2 Spieler) ![]() (Autor:
Daniel Garmann, Bergisch-Gladbach)
(Autor:
Daniel Garmann, Bergisch-Gladbach)
Die Daten liegen in einer linearen Struktur vor, in einem Array (Feld) oder in verketteten Listen.
(Man stelle sich zum Beispiel einen Stapel Bilder vor, in dem man ein bestimmtes Bild sucht.)
Wir gehen davon aus, dass jedes Element nur einmal vorkommt.
Man vergleicht den Suchschlüssel mit den Elementen, beginnend beim ersten. Entweder man findet eine Übereinstimmung, oder man ist am Ende des Feldes angelangt - in beiden Fällen wird die Suche beendet.
Als Ergebnis erhält man eine Meldung: der Suchschlüssel ist enthalten oder: der Suchschlüssel steht an einer bestimmten Position des Feldes.
best case: a[1] = x, die Schleife wird nicht durchlaufen
worst case: Schleife wird (n-1) mal durchlaufe, x kommt im Array a nicht vor
Ein Array enthält Elemente, zum Beispiel Zahlen, die der Größe nach aufsteigend sortiert sind. Nach einem bestimmten Element x wird folgendermaßen gesucht: das Array wird in jedem Schritt in der Mitte geteilt und das rechts neben der Mitte stehende Element wird mit dem Suchelement x verglichen.
Ist x < b, wird in der linken Hälfte weiter gesucht,
ist x > b, wird in der rechten Hälfte gesucht,
ist x = b, ist x gefunden.
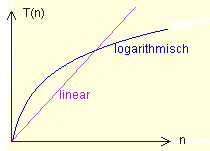 |
Wie hier ersichtlich, wächst die logarithmische Funktion asymptotisch schwächer als die lineare. |
![]() AB
AB
![]() interaktive Animation (empfehlenswert) (untere Lerneinheit anklicken)
interaktive Animation (empfehlenswert) (untere Lerneinheit anklicken)
![]() Folien zur binären Suche (empfehlenswert)
Folien zur binären Suche (empfehlenswert)
![]() Exkurs "Weitere Informationen zur binären Suche"
Exkurs "Weitere Informationen zur binären Suche"
Man stelle sich vor, in einem 300 Seiten starken Buch die Seite 70 zu suchen. Man wird das Buch also weiter vorn, im ersten Drittel, aufschlagen. Man trifft vielleicht auf die Seite 96. Nun schlägt man etwa ein Drittel weiter nach vorn und ist bestimmt schon ganz nah der gesuchten Seite. Dieses Vorgehen wird solange fortgesetzt, bis man auf Seite 70 gelandet ist.
Die Unterteilung der Suchintervalle geschieht also durch genaue Abschätzung des Unterteilungspunktes.
Während man bei der binären Suche den Array in der Mitte teilt, wird bei der Interpolationssuche die erwartete oder wahrscheinliche Suche abgeschätzt.
Aufwand: Sind die Schlüsselwerte n relativ gleich verteilt (etwa wie die Seitenzahlen in einem Buch), beträgt der Aufwand im Mittel O(log log n). Zu beachten ist jedoch, dass in der Praxis der Berechnungsaufwand für m groß ist.
Hier wird eine Übersetzungstabelle genutzt. Mit dieser Hash-Tabelle kann man schnell auf jedes gesuchte Element einer Liste zugreifen.
Ein Beispiel ist im Unterricht besprochen worden:
MONTAG DIENSTAG MITTWOCH DONNERSTAG FREITAG SAMSTAG SONNTAG
Für diese Elemente werden jetzt Schlüssel angelegt.
Eine Vorschrift zur Bildung dieser Schlüssel könnte lauten:
Nr. des 1. Buchstaben im Alphabet + Nr. des 2. Buchstaben-10
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
9. |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
Das würde für MONTAG bedeuten: M O
13 + 15 -10 = 18
Problematisch würde es, wenn man SONNABEND statt SAMSTAG hätte, dann würde es, wie man sagt, zur Kollision wegen gleicher Schlüssel kommen. (Abhilfe hier)
Beispiel 2
Schüler einer Klasse
| Alois Sintermann | AS | ergibt | (1,19) |
| Bärbel Bommel | BB | (2,2) | |
| Konrad Licht | KL | (11,12) | |
| Adelheid Fechter | AF | (1,6) |
Hash-Tabelle mit den Schlüsseln, die auf konkrete Speicherplätze der Daten verweisen
| 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10 | 11 | 12 | ... | |
| 1 | |||||||||||||
| 2 | |||||||||||||
| 3 | |||||||||||||
| 4 | |||||||||||||
| 5 | |||||||||||||
| 6 | |||||||||||||
| 7 | |||||||||||||
| 8 | |||||||||||||
| 9 | |||||||||||||
| 10 | |||||||||||||
| 11 | |||||||||||||
| 12 | |||||||||||||
| 13 | |||||||||||||
| 14 | |||||||||||||
| 15 | |||||||||||||
| 16 | |||||||||||||
| 17 | |||||||||||||
| 18 | |||||||||||||
| 19 | |||||||||||||
| ... |
Wegen der 26 Buchstaben des Alphabets bekommen wir ein Array der Länge 26 x 26 und können damit auf jeden Schüler zugreifen. Dies funktioniert zunächst nur, wenn alle Schüler dieser Klasse unterschiedliche Initialen haben. Kommt zum Beispiel der Schüler Börge Blind neu in die Klasse, käme es wieder zur Kollision (hashtabellenmäßig ;-)).
Es geht also darum, mithilfe eifacher Rechenoperationen die Speicherstelle eines Elements aus seinem Schlüssel berechnen zu können.
Hier verwendet man zwei Hashfunktionen. Mit der einen wird die Hashadresse eines Schlüssels in der Tabelle gesucht, mit der anderen wird (bei Kollision) in der Tabelle der nächste freie Platz gesucht.
Wenn der Platz in der Tabelle einen Füllstand übersteigt, muss sie vergrößert werden und alle Elemente müssen neu zugeteilt werden. Dies nennt man Rehashing.
An dieser Stelle empfehle ich folgende Animation (Lautsprecher einschalten!) ![]()
Für besonderes Interessierte ;-):
Bucket Hashing (Aufteilen des Arrays in verschiedene buckets)
Separate Chaining (Jedes Element der Hash-Tabelle hat einen next-Zeiger auf eine verkettete Liste - wird auch in der Animation gezeigt)