Sortierverfahren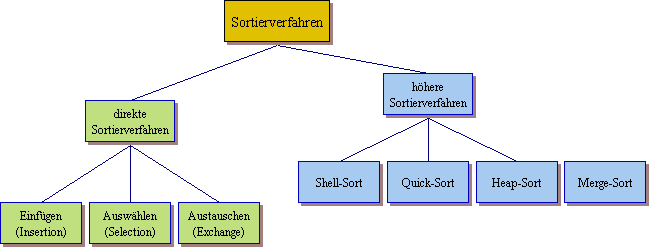

Begriff

Eine Menge von Daten (Objekte) wird in eine definierte Ordnung gebracht - auf- oder absteigend,
mit größer/kleiner - Relation (z. Bsp. Primzahlen) oder lexiografischer Relation (z. Bsp. Telefonbuch). Das geht nur, wenn diese diese objektiv zueinander vergleichbar sind.

 

Zweck des Sortierens

Mögliche Ergebnisse von Sortiervorgängen

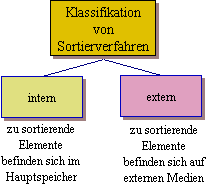
Klassifikation
- Übersichtlichkeit (Minimum / Maximum / Anzahl der daten / Häufigkeitsverteilung)
- Vorsortierung für effiziente Suchverfahren
- Verwaltung indizierter Daten

Komplexität

Untersucht wird hier das Verhältnis der Anzahl vor allem der Vergleichs- und Umstelloperationen zur Anzahl der zu sortierenden Daten.

C(n) bedeutet Anzahl der Schlüsselvergleiche,
M(n) bedeutet Anzahl der Elemente-Umstellungen,
O(n) die Ordnung; so sind die Komplexitäten von C(n) oder/und M(n) von der Ordnung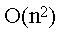. Bei höheren Sortierverfahren ist die Komplexität günstiger.
Vergleichsbasierte Sortierverfahren haben mindestens die Komplexität O(n log(n)).

siehe auch
Vergleich 1 von Sortierverfahren

Vergleich 2 von Sortierverfahren (Alle Demos per Doppelklick starten)

Selection-Sort

Sortieren durch Auswählen (mitunter MinSort genannt)

Algorithmus

Gegeben sei ein Array mit n Elementen, das in aufsteigender Reihenfolge sortiert werden soll:

"Hole jeweils das kleinste Element nach vorne''
(Im Unterricht wurden Schüler nach ihrer Körpergröße sortiert ;-))

Das Array besteht also aus einem sortierten vorderen Teil, der in jedem Schritt um ein Element wächst, und einem unsortierten hinteren Teil, der entsprechend schrumpft. D.h. bei der Suche nach dem x-kleinsten Element muss nur noch der unsortierte hintere Teil des Arrays ab dem x-ten Element durchsucht werden, da die ersten x-1 Elemente bereits sortiert sind. Genauer gesagt, muss in jedem Schritt jeweils das kleinste Element des unsortierten Teils gesucht und mit dem ersten Element des unsortierten Teils vertauscht werden.

Zur Demonstration der Wirkungsweise werden hier zwei Möglichkeiten empfohlen: PowerPoint , Applet

Aufgabe a) Übernehmen Sie das Beispiel aus Wikipedia, ersetzen Sie jedoch die Buchstaben durch Zahlen!
Aufgabe b) Ermitteln Sie in dem Programm die durchschnittliche Laufzeit bei 10 Sortiervorgängen (Tabelle!)! [5 BE]

Analyse

Um das Minimum zu bestimmen, benötigt Selection-Sort n-1 Durchläufe.
Beim ersten Mal benötigt das Bestimmen des Minimums n-1 Vergleiche, beim zweiten Mal n-2 usw.

Die mittlere Laufzeit (Theta) von Selection-Sort ist quadratischer Ordnung.

 

Quick-Sort

Ein ausgewähltes Element ist an die ausgewählte Arrayposition zu bringen. Dazu sind n-1 Vergleiche notwendig.

11
  
03
  
21
  
42
  
08
  
07
 
11 sei das ausgewählte Element ai. Bei der Suche von links ist die 21 das erste Element > 11. Diese wird in die linke Hand genommen. Nun beginnt von rechts die Suche bis zu dem Element, das kleiner (oder gleich) als 11 ist. Dieses - die 07 - wird in die rechte Hand genommen. Nun werden 21 und 07 miteinander getauscht.
11
  
03
  
07
  
42
  
08
  
21
 
Nun wird wieder von links aus gesucht und zwar bei der Position, die im vorigen (linken) Durchlauf noch nicht betrachtet wurde. Das Element 42 wird in die linke Hand genommen und es wird nun von rechts gesucht, beginnend bei der Position, die noch nicht besucht wurde. Also wird 08 in die rechte Hand genommen und beide Elemente werden miteinander getauscht.
11
  
03
  
07
  
08
  
42
  
21
 
Wenn sich in der Fortsetzung dieses Prozesses linke mit rechter Suche kreuzt , wird das Element in der linken Hand zurückgelegt, das der rechten mit dem zu Beginn gewählten Element hier die 11 - getauscht.
08
  
03
  
07
  
11
  
42
  
21
 
Element 11 ist nun auf dem endgültigen Platz. Nacheinander wird nun das Verfahren für den Bereich links von der 11 und für den Bereich rechts von der 11 separat angewendet. (-> Rekursion)
07
  
03
  
08
  
11
  
21
  
42
 
Element 11 ist nun auf dem endgültigen Platz. Nacheinander wird nun das Verfahren für den Bereich links von der 11 und für den Bereich rechts von der 11 separat angewendet. (-> Rekursion)
03
  
07
  
08
  
11
  
21
  
42
 
Element 11 ist nun auf dem endgültigen Platz. Nacheinander wird nun das Verfahren für den Bereich links von der 11 und für den Bereich rechts von der 11 separat angewendet. (-> Rekursion)

 

- Suche links links von ai ein Element, das größer als ai ist.

- Suche rechts rechts von ai ein Element, das kleiner als ai ist.

- Wenn beide Elemente gefunden: vertauschen

- Wenn nur ein Elemenent gefunden: mit ai vertauschen


Erläuterung und Animation (empfehlenswert) , hier als Archiv