Heap (Halde, Haufen)
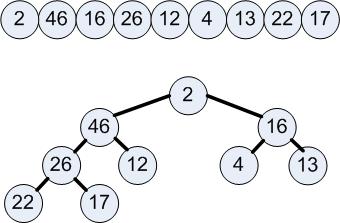
Vor dem eigentlichen Sortieren wird erst aus dem unsortierten Array erst einmal ein Heap aufgebaut: ein binärer Baum wird mit den Elementen der Folge gefüllt.
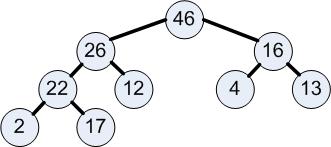
In einem Heap (rechte Abb.) ist der Wert der Söhne jedes Knotens immer kleiner als der Wert des Knotens selbst. Der größte Wert steht stets in der Wurzel (im Beispiel 46).
1. Aus der Eingabefolge von sortierbaren Elementen wird ein binärer Baum konstruiert.
2. In diesem binären Baum wird beim sogenannten Versickern so lange ein Knoten mit dem größeren seiner Söhne vertauscht,
bis das größte Element an der Wurzel steht. Das Ganze wird Heap genannt..
3. Das Element mit dem kleinsten Wert, also das letzte, das am tiefsten sitzende Blatt, kommt auf die Stelle der Wurzel.
Nun wandert das Element von der Wurzel in das Array.
4. Weiter mit 2., bis die Wurzel leer ist.
Komplexität:
- Aufbau des Heaps in O(n) Schritten
- Versickern eines Elements von der Wurzel: O(n log n) Schritte
- Insgesamt: O(n log n)
- Worst case:
Die Daten sind weitgehend vorsortiert. O(n log n)
Dazu muss man wissen, dass der Aufbau des Heaps eine schrittweise vollständige Umkehrung der Sortierreihenfolge darstellt.
- Best case: - Datenfeld liegt bereits in umgekehrt sortierter Weise vor - 1 Vergleich pro Element, keine Zuweisung.
Das ist sehr unwahrscheinlich.
- Oder: Fast alle Daten sind identisch.
a) Dieser schnelle Sortieralgorithmus ist hier  schön anhand eines Lernprogramms (Download möglich) erklärt. Es ist ratsam, sich einige Seiten auszudrucken. b) Laden Sie sich diese Animation (Powerpoint) herunter und verfolgen Sie die enzelnen Schritte! c) Anschaulicher ist wohl aber die Grafik (Sortieren von Zahlen oder von Buchstaben) bei Wikipedia . d) Notieren Sie sich den Ablauf von dieser Seite: (Dort ist auch eine Animatuion zu finden.)e) Geben Sie Elemente in dieses Applet ein und verfolgen Sie den Algorithmus!f) Wahrscheinlich ist diese Animation am einprägsamsten: !g) Drucken Sie dieses Arbeitsblatt  aus und üben Sie das Ordnen und anschließende Sortieren. |