NP-schwere Probleme

Die Klasse P - praktisch lösbare Probleme - also Entscheidungsprobleme, die in Polynominalzeit in einer deterministischen Turing-Maschine gelöst werden können. (Deteministisch bedeutet, dass der nächste Schritt ist eindeutig bestimmt ist.) Es gibt ein bestimmtes Programm, und genau das wird von der Turing-Maschine abgearbeitet, irgendwann wird dann das Ergebnis ausgegeben. Die Klasse P ist eine Teilmenge von NP, ob sie mit NP identisch ist, ist unklar, vermutlich nicht.

Klassifizierung von Entscheidungsproblemen

Die Klasse NP - nicht-deterministisch entscheidbare Probleme (Nicht-deterministisch bedeutet, dass der nächste Schritt nicht eindeutig bestimmt ist.) - Probleme, die von einer nichtdeterministischen Turing-Maschine in polynomialer Zeit entschieden werden können Man kann also die Lösungskandidaten effizient überprüfen. Eine nicht-deterministische Turing-Maschine hat die Möglichkeit, zu "raten", wie sie weiter vorgeht, d.h. welchen Befehl sie ausführt. Probleme, die das n im Exponenten haben, und auch die Probleme, die von der "ratenden" TM gelöst werden, gehören also zur Klasse NP. Podcast

NP-vollständige Probleme
So bezeichnet man die schwersten Probleme in der Klasse NP, zur Zeit etwa 2000.
Sie sind entscheidbar.
Es ist ein Polynomialzeit-Algorithmus zur Überprüfung der Lösung bekannt.
Sie besitzen Lösungen in exponentieller Zeit. Niemand konnte jedoch bislang beweisen, ob sie exponentielle Zeit benötigen müssen.
Sie sind ausführbar, wenn man zeigen kann, dass irgend ein NP-vollständiges Problem ausführbar ist (dass es durch einen polynomialen Algorithmus gelöst werden kann). Polynomiale Algorithmen für solche Probleme kennt man bislang nicht, man nimmt an, dass es diese auch nicht gibt. Das müsste "nur" noch bewiesen werden.
Sie sind miteinander verwandt. (Darauf bezieht sich die Formulierung "vollständig".) Sollte jemand einen Polynomialzeit-Algorithmus zur Lösung eines einzigen NP-vollständigen Problems finden, würde sich dies auch auf alle anderen NP-vollst. Probleme anwenden lassen.

Bsp.: TSP, Stundenplanproblem
Podcast | Podcast | Podcast Millenium Problems

Glossar zu dem nachfolgenden Text
adjazent - Knoten sind miteinander verbunden, benachbart.
inzident - Eine Kante ist mit einem Knoten inzident, wenn die Kante von dem Knoten weg- oder hinführt.
G - ungerichteter Graph
E - Kantenmenge
V - Knotenmenge
U - Teilmenge, Knotenüberdeckung von G
Knotenüberdeckung - Eine Knotenüberdeckung ist eine Teilmenge der Knoten eines Graphen, die insgesamt mit allen Kanten inzident sind.
Informationen
Weitere Informationen:

Bevor Sie anfangen: Wie wär's mit einer Million Dollar? Das ist kein Scherz!

Laden Sie sich bitte ein Programm, mit dem schnell Graphen erstellt und bearbeitet werden können, aus dem Internet:

Das Cliquenproblem (clicque)

Hefteintrag

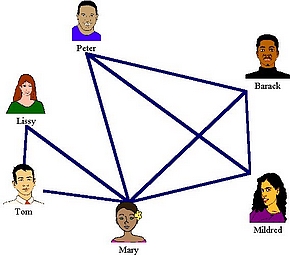In diesem ungerichteten Graph gibt es viele Cliquen. Jede Zweiergruppe ist eine Clique, aber auch Lissy, Tom und Mary oder Peter, Barack Mildred und Mary. Die größte Clique ist in diesem Graph die letztgenannte. Allgemein: Eine Clique der Größe k  - k-Clique) - in einem Graphen G = (V, E) ist ein vollständiger Teilgraph der Größe k. Vollständig bedeutet in unserem Fall, dass sich die Mitglieder einer Clique untereinander kennen, durch eine Kante verbunden sind. Die Größe einer Clique ist die Anzahl der in ihr enthaltenen Knoten. Im Beispiel ist k = 4 für die größte Clique. Beim Cliquenproblem geht es um Optimierung, nämlich darum, eine Clique maximaler Größe in einem Graphen zu bestimmen. Das bezieht sich natürlich auf Graphen mit einer nicht mehr überschaubaren Anzahl an Knoten. Formal: Wonach kann nun gesucht werden? a) Gibt es in einem Graphen eine Clique der Größe k? - Entscheidungsproblem b) Berechne das größte k, sodass der Graph eine k-Clique enthält. - Optimierungsproblem c) Berechne eine maximale Clique des Graphen. - Optimierungsproblem

Soll die maximale Größe einer Clique bestimmt werden, so sind alle Teilmengen des Graphen zu erzeugen und diese jeweils darauf zu überprüfen, ob sie eine Clique sind. Das ist nicht effizient, weil es Kandidaten gibt. Ein Test verläuft vergleichbar schnell, da maximal Paare zu testen sind. Optimierungs- problem Aufgabe a) Wie groß ist die größtmögliche Clique? Geben Sie die Bezeichnungen der entspr. Knoten an! Optimierungs- problem Aufgabe b) Finden Sie eine maximal große Clique! Entscheidungs- problem Aufgabe c) Gibt es eine Clique >= k für (G,3), für (G,5)?         Entscheidungs- problem Aufgabe d) Die Clique der orange markierten Knoten hat die Größe k=3. Finden Sie die größte Clique! Aufgabe e) Finden Sie eine maximal große Clique! V' = {......................} Aufgabe f) Zeichnen Sie einen 8-knotigen Graph , so dass jeder Knoten zu einer 3er Clique gehört!

Reduktion von Clique auf Knotenüberdeckung

Der Graph enthält die Clique V' = {1,2,3,4}.	Durch Reduktion wird dieser Graph erzeugt, der die Knotenüberdeckung V-V' = {5,6} besitzt.

Aufgabe h) Reduzieren = transformieren Sie den Graphen nach vertex cover = Knotenüberdeckung, indem Sie den Komplementgraphen zeichnen d.h. zwischen die Knoten Kanten setzen, zwischen denen bislang keine Kanen waren. Die Knoten links, die nicht zur Clique gehören, bilden dann im Komplementärgraphen die Überdeckungsknoten (diejenigen, in denen je eine Überwachungskamera installiert wird ;-)).

Aufgabe i) Üben Sie mit dem Programm graphbench.

Das Knotenüberdeckungsproblem (vertex cover)  
(NP-vollständig)

Eine Schauspielerin möchte eine stressfreie Party anlässlich ihres 40. Geburtstages feiern. Bevor sie die Einladungen verschickt, schreibt sie noch schnell auf, wer sich mit wem nicht verträgt: (A,D), (B,D), (B,E), (C,E), (D,F), (D,E), (E,G), (F,G), (F,H). Nun versucht Irene, das Problem grafisch darzustellen. Mit Entsetzen stellt sie fest, dass nur Adelheid, Heinz und Carola infrage kommen. Naja, Hauptsache harmonisch ;-) (Die Namen sind rein zufällig gewählt! We.)
Was wird eingegeben? - ein ungerichteter Graph G wie nebenstehend - eine positive natürliche Zahl k (G setzt sich aus der Knotenmenge V (set of vertices) und der Kantenmenge E (set of edges) zusammen: G = (V,E) Was ist zu tun? Es ist eine Teilmenge von Knoten V' von V zu finden, so dass jede Kante aus E mind. einen Knoten in V' hat. In V' sind nicht mehr als k Elemente. Als Ergebnis erhält man die Teilmenge V', das ist die Knotenüberdeckung von G.	A B C D E F G H A 0               B 0 0             C 0 0 0           D 1 1 0 0         E 0 1 1 1 0       F 0 0 0 1 0 0     G 0 0 0 0 1 1 0   H 0 0 0 0 0 1   0 Adjazenzmatrix
Je mehr Knoten und Kanten wir jedoch zu berücksichtigen haben, desto schwieriger wird es, eine Teilmenge V' (Knotenüberdeckungsmenge) zu finden. . Die Knotenmenge V besitzt Teilmengen, in Irenes Fall wären dies = 256 Teilmengen. Besitzt der zu untersuchende Graph n Knoten und m Kanten, so sind für jede Teilmenge V' maximal n * m Prüfschritte möglich, im Beispiel also 72 (wegen 8 Knoten * 9 Kanten). Knotenüberdeckung: Enthält jede Kante von E einen Knoten aus V', so nennt man V' eine Knotenüberdeckung von G. Knotenüberdeckungszahl: Die Anzahl der Knoten einer kleinsten Knotenüberdeckung von G.
Problematisch wird es bei um die 100 Knoten. Rechne doch mal aus, wie lange ein Computer für n = 100 braucht, wenn er pro Sekunde 1000 000 Fälle untersucht. Der Aufwand ist so groß, dass man ihn sich gar nicht mehr vorstellen kann ;-)
Eine von mehreren Lösungsmöglichkeiten, die zwar nicht optimal, aber doch in absehbarer Zeit möglich ist, besteht darin, die Knoten mit den meisten Kanten zu eliminieren und dies zu wiederholen bis zur Löschung aller Graphkanten. Vgl. "Das Knotenüberdeckungsproblem - eine Fallstudie zur Didaktik NP-schwerer Probleme", in: JENAER SCHRIFTEN ZUR MATHEMATIK UND INFORMATIK, 2006 Aufgabe a) Eine Übung: --Applet Aufgabe b) Üben Sie mit dem Programm graphbench. Approximative (=Näherungs-) Lösungen mit polynomialer Laufzeit erhält man mit dem Approx-Vertex-Cover-Algorithmus. Infos unter sowie unter , S. 7/8. Letzteres Beispiel stammt ursprünglich aus dem Cormen, S. 1027f.

Das Behälterproblem (bin packing)
(NP-vollständig)

Unterschiedlich große Gegenstände sind in möglichst wenigen Behältern unterzubringen.Die Behälter haben die gleiche Größe.
Variante offline: Anzahl und Größe der Gegenstände sind bekannt. Die Verteilung auf die Behälter ist fast ideal möglich.
Variante online: Nur der aktuelle Gegenstand ist bekannt, die beliebig vielen anderen nicht. Es muss aber sofort verpackt werden. Somit kann man nur eine Annäherung an die ideale Verteilung erzielen.

Entscheidungsproblem (NP-vollständig)
Gegeben: n, k. Können die n Gegenstände so auf die k Behälter verteilt werden, dass keiner der Behälter überläuft?

Optimierungsproblem (NP-schwer)
Finde eine Zuordnung, bei der die Anzahl an Behältern minimiert wird.

Kann ein Entscheidungsproblem in polynomialer Zeit nicht gelöst werden, dann kann auch das zugehörige Optimierungsproblem nicht in polynomialer Zeit gelöst werden.

Wo spielen Behälterprobleme eine Rolle?
- Verpackungsmittelindustrie

Aufgabe a) Eine Übung: --Applet

Lösungsmöglichkeiten

Next Fit

Ein Behälter wird solange mit Gegenständen befüllt, bis ein Gegenstand zu groß ist. Jetzt wird der aktuelle Behälter geschlossen und ein neuer Behälter bereitgestellt, in den der Gegenstand hineinkommt. Es kann sein, dass der erste Behälter nicht ganz voll ist - Deckel drauf, dann sieht's keiner. Natürlich kann next Fit zu einer sehr ungünstigen Verteilung führen. Laufzeitverhalten: linear (Es geht schnell, verbraucht aber viele Eimer ;-))

First Fit

Das aktuelle Element wird in den ersten Behälter gepackt, in den es hineinpasst. Prinzip: kein Platz wird verschwendet! Die Deckel müssen aber, solange die Behälter nicht gefüllt, daneben liegen.
Im schlimmsten Fall muss man alle Behälter nach dem passenden Platz durchsuchen - die Laufzeit ist in O(n²) , es sei denn, man organisiert die Behälter in Bäumen, dann beträgt die Laufzeit O(n log n).

Aufgabe b) Dieses -Applet demonstriert First Fit.

Best Fit

Hier wird der Gegenstand nicht in den ersten Behälter gepackt wird, in den er hinein passt, sondern in den vollsten.

Aufgabe c) Lesen Sie sich den Text auf der Seite aufmerksam durch. Auch als

Das Rucksackproblem (knapsack)  
(schwach NP-vollständig)

Aufgabe a) Der interaktive Rucksackproblem-Löser Wer ist der beste Outdoor-Spezialist des Kurses?

Hefteintrag:

Beispiele für das Rucksackproblem
- Der Einkauf ist auf zwei Einkaufstaschen derart zu verteilen, dass diese gleich schwer sind.
- Aupair Madleen hat folgende Aufgaben aufgeschrieben bekommen:
  Wohnung putzen, einkaufen, ein Vier-Gänge-Menu kochen, Kinder duschen, Hund ausführen,
  Kleid aus der Reinigung holen, Kinder für Karneval schminken. Welche Reihenfolge ist die günstigste?
- Funkkom plant ein neues Mobilfunknetz mit 5.000 Antennen und 100 verschiedenen Frequenzen.
  Kann man das so einrichten, dass alle benachbarte Antennen auf verschiedenen Frequenzen senden?

Nun gilt es, in Einzelarbeit 5 Aufgaben zu lösen:

Aufgabe b) Lesen Sie den ersten Textabschnitt , denken Sie sich ein eigenes Beispiel aus und schreiben Sie anhand dieses Beispiels, was unter "Rucksackproblem" zu verstehen ist.

Aufgabe c) Erklären Sie die Begriffe "Gewichtsschranke" und "Profitdichte"!

Aufgabe d) Wie viele Möglichkeiten gibt es bei 10 Gegenständen, die zur Befüllung des Rucksacks zur Verfügung stehen? Schreiben Sie einen Antwortsatz unter Einbeziehung der Fragestellung.

Aufgabe f) Zeichnen Sie sich ein ähnliches Diagramm wie auf der Seite ab, tragen Sie einige blaue und rote Punkte ein und erklären Sie dazu den Begriff Pareto-optimale Punkte!

Die fertige Word-Datei ist an heidecksburg@web.de unter dem Betreff RSP zu schicken.

HA

Aufgabe g) Eine andere Seite: Angenommen, es gilt, 50 Gegenstände unterzukriegen. Wie alt sind Sie, wenn der Rechner fertig mit dem Berechnen ist? Schreiben Sie einen Antwortsatz unter Einbeziehung der Fragestellung.

Spiel(e)

Lösung mittels eines Quantencomputers möglich?

Das Hamiltonkreisproblem (hamiltonian circuit)
(NP-vollständig)

Ein Hamilton Kreis ist ein Pfad, der jeden Knoten genau einmal besucht. Die Entscheidungsfrage ist nun, ob es in einem Graphen solch einen Hamiltonkreis gibt.

Man stelle sich Neustadt einfach als einen Graphen vor: Die Kreuzungen sind die Knoten und die Straßenabschnitte zwischen diesen Knoten sind die Kanten. Eine Reisegruppe soll nun auf einem Weg an allen Sehenswürdigkeiten vorbeigeführt werden.

Lösungsmöglichkeit: Backtracking (für wenige Knoten)
- Beginne bei einem Knoten - meinetwegen bei der Stadtkirche - und speichere die Pfade zu unbesuchten Sehenswürdigkeiten, ausgehend von der Kirche.
- Für jeden Pfad sind neue Pfade - ausgehend vom letzten Knoten - zu unbesuchten Nachbarn zu speichern.
- Wiederhole diese Schritte, bis ein Hamilton Kreis gefunden wird oder bis alle Pfade besucht wurden oder du vor Müdigkeit auf einer Parkbank einschläfst.

Anmerkung: Man unterscheidet beim Hamiltonkreisproblem zwischen ungererichteten und gerichteten Graphen.

Aufgabe b) Üben Sie mit dem Programm graphbench.

Das Problem des Handelsreisenden (traveling salesman problem)
(NP-vollständig)

Wer von Neustadt an der Orla nach Rostock will, gibt die beiden Orte ins Navi ein und erhält binnen Sekunden die optimale Route. Sollen auf dem Weg noch Berlin, Magdeburg, Salzwedel und Neubrandenburg in dieser Reihenfolge angefahren werden, berechnet die Elektronik erst den besten Weg von Neustadt an der Orla nach Berlin, dann die Strecke von Berlin nach Magdeburg usw..

Problematisch wird es, wenn in beliebiger Reihenfolge mehrere Städte besucht werden sollen, dabei aber auf dem kürzesten Gesamtweg. Möchte ein Duhlendorfer bei allen Karnevalshochburgen – nehmen wir an, es sind 26 - auf einer möglichst effizienten, also preisgünstigen Rundreise vorbeischauen, wären die schnellsten Computer der Welt mit der Reiseplanung hoffnungslos überfordert. Angenommen, es gäbe zwischen den Städten immer nur eine Verbindung, sind über 1 000 000 000 000 000 000 000 000 Routen möglich. Aber diese Rechnung ist viel zu aufwändig. Eine Million Dollar wurden von der Clay Foundation ausgelobt.

Aufgabe b): Markieren Sie einige Punkte für eine Rundreise in Ihrer Heimat auf der Karte und lassen Sie sich die Rundreise (z.Bsp. Sehenswürdigkeiten) vorführen.

Aufgabe d): Planen Sie auf einer Karte eine Rundreise (Auto oder Flugzeug, speichern Sie das Bildschirmfoto!

Aufgabe e): Arbeiten Sie die Erläuterung durch und schauen Sie sich dieses Applet an! Applet zur Demonstration des Ameisen-Alg. und des Abkühlungsprozess-Alg.:

Aufgabe g) Üben Sie mit dem Programm graphbench.

Das Färbeproblem (chromatic number)  
(3-color ist NP-vollständig)

Stellen Sie sich vor, Sie haben Biologie im Fachraum, plötzlich drängt eine 5. Klasse herein, deren Schüler lautstark behaupten, jetzt hier Biologie zu haben und zu ihrer Rechtfertigung auf den Vertretungsplan verweisen. Dieses Problem fällt unter die sogenannten Färbeprobleme. Jede Klasse hat auf dem Plan eine bestimmte Farbe, dazu jeder Raum und jeder Lehrer. Hinzu kommt, dass durch Hallenbelegungszeiten und durch Blockunterricht im Kurssystem weitere Faktoren auf den Stundenplanbau wirken. Bis heute gibt es kein Programm, das dieses Problem optimal lösen kann.
Beim Färben von Karten versucht man mit minimaler Anzahl an Farben auszukommen.

Aufgabe e) Üben Sie mit dem Programm graphbench.

Eulerformel: Für jeden planaren zusammenhängenden Graphen G = (V,E) gilt
|V| - |E| + |A| = 2     

(A - Flächen, E - Kanten, V - Knoten)

Vier-Farben-Satz

4 Farben reichen immer aus, um eine beliebige Landkarte in der euklidischen Ebene (zweidimensional) so einzufärben, dass keine zwei angrenzenden Länder die gleiche Farbe bekommen.
(Ein gemeinsamer Punkt zählt nicht als Grenze.)

Einige weitere Problemchen:
Mengenpackungsproblem, Mengenüberdeckungsproblem, Steinbauerproblem, Maximaler Schnitt

Ein Spielchen gefällig?