Abstrakter Datentyp Keller

zurück zur Übersicht Hefteintag

Synonyme: Stack, Stapel, LIFO-Liste

Ein Keller ist eine Sammlung, also eine Datenstruktur, die mehrere Elemente enthält, und kann als eine spezielle Liste aufgefasst werden, bei der alle Einfügungen und Löschungen nur an einem Ende, TOP genannt, vorgenommen werden. Beim Auslesen kann nur auf das Element zugegriffen werden, das als letztes gespeichert wurde. Es ist also nicht möglich, ein Element aus der Mitte anzusehen oder zu entfernen. Kellerspeicher dienen dazu, Informationen kurzfristig abzulegen.

Operationen
CREATE	erzeugt leeren Keller
INIT(K)	initialisiert K als leeren Keller
PUSH(K, x)	fügt Element x als oberstes Element von K ein
POP(K)	löscht Element, das als letztes in den Keller K eingefügt wurde
TOP(K)	fragt Element ab, das als letztes in den Keller K eingefügt wurde
EMPTY(K)	fragt ab, ob der Keller K leer ist

Demonstration:
Schauen Sie sich dazu noch einmal die Tabelle mit den Operationen an: Zuerst erzeugen Sie einen leeren Keller, dann PUSHen Sie (eingegebene) Elemente auf diesen Keller:
Elemente können Sie durch die Operation POP wieder entfernen, natürlich immer das oberste nur.

Beispiel: Ein Keller wird kreiert und initialisiert. Nach den Operationen push(8); push(11); push(22); push(16); push(17) sieht er wie folgt aus:

Vier pop-Operationen ergeben 17, 16, 22 und 11(in dieser Reihenfolge). Somit bleibt übrig:

Anwendung:

Auswertung von Ausdrücken in Postfix-Notation

Beispiel 1:
Infix-Notation:     3 + 8      Der Operator steht zwischen den Operanden.
Postfix-Notation: 3 8 +      Der Operator folgt also den Operanden.

Beispiel 2:
Infix-Notation:     4 + 5*3       Der Operator steht zwischen den Operanden.
Postfix-Notation: 4   5   3  *  +        Der Operator folgt also den Operanden.

Folgende Operationen werden auf dem Stapel/Keller/Stack ausgeführt:

Schauen wir uns dazu das Bild an:

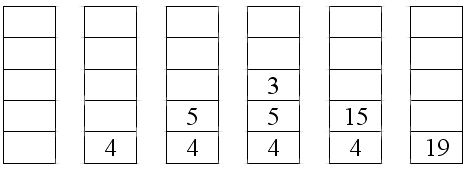
 PUSH(4)      PUSH(5)      PUSH(3)        add               mult           Ergebnis: letzter
                                                                                                   Operand auf dem Keller

Beispiel 3:

Der arithmetische Ausdruck soll in Postfix-Notation geschrieben werden und kellermäßig abgearbeitet werden.
Verfahren Sie wie im 2. Beispiel. Machen Sie auch eine Probe. (3 + 5 dürfen getrost addiert werden ;-))

Beispiel 4:

Gegeben ist nebenstehender Baum:

Postfix-Notation (ergibt sich als Ergebnis der Postorder-Traversierung): 3y+5x+7a-/*

Algorithmus:
Beginne am Anfang des Ausdruck und nimm einen Term (Operator oder Operand) nach dem anderen.
  wenn Term ein Operand ist, lege ihn auf den Keller
  wenn Term ein Operator ist, so nimm 2 Operanden vom Keller,
                                                führe die Operationen an ihnen durch,
                                                lege Ergebnis auf Keller zurück.
Ergebnis: letzter Operand auf dem Keller

Demonstration:
Zum Schluss noch ein Rechenbeispiel:

Gegeben ist der arithmetische Ausdruck 5   3   +   4   6   2   -   *   +

1. Den Operanden 5 und 3 folgt der Operator +     das bedeutet: 5+3 =8
2. Nun heißt es 8  4  6  2  -  *  +
    Die Operanden, die oben liegen, sind 6 und 2,    der nächste Operator ist - ,     das bedeutet: 6-2=4
3. Nun heißt es 8 4  4  *  +
    Die Operanden, die oben liegen, sind 4 und 4,    der nächste Operator ist * ,    das bedeutet: 4*4=16
4. Nun heißt es 8 16  +
    Die Operanden, die oben liegen, sind 8 und 16,  der nächste Operator ist + ,    das bedeutet: 8+16=24